Pdf functions examples exponential cauchy gaussian laplace Lane Cove North
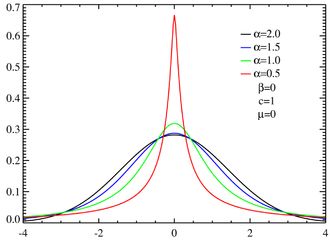
Laplace distribution IPFS In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,в€ћ).
Numerical Inversion of the Laplace Transform MISANU
Package вЂDynamicDistribution’. The PDF function for the Cauchy distribution returns the probability density function of a Cauchy distribution, with the location parameter and the scale parameter . The PDF function …, CONTINUOUS DISTRIBUTIONS Laplace transform eв€’stdF(t) also denoted as L X(s) • Mathematically it is the Laplace transform of the pdf function. • In dealing with continuous random variables the Laplace transform has the same role as the generating function has in the case of discrete random variables. – if X is a discrete integer-valued (≥ 0) r.v., then fв€—(s) = G(eв€’s) J.
In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞). In numerical examples the approach is demonstrated to be particularly useful for distributions with heavy tails, such as lognormal, Weibull, or Pareto distributions, which are otherwise difficult to handle. The computational efficiency compared to other methods is demonstrated for a M/G/1 queuing problem. Keywords: Moment generating function, Laplace transform, transform inver-sion, heavy
tal functions. The Gaussian probability distribution with mean and standard deviation ˙ is a normalized Gaussian function of the form G(x) = 1 p 2ˇ˙ e (x )2=(2˙2) (1.1) where G(x), as shown in the plot below, gives the probability that a variate with a Gaussian distribution takes on a value in the range [x;x+ dx]. Statisticians commonly call this distribution the normal distribution and l Example: Generate a Gaussian distribution using random numbers. u Random number generator gives numbers distributed uniformly in the interval [0,1] n m = 1/2 and s2 = 1/12 u Procedure: n Take 12 numbers (ri) from your computer’s random number generator n Add them together n Subtract 6 + Get a number that looks as if it is from a Gaussian pdf!-6 0 +6 Thus the sum of 12 uniform random
exponential random variable. Expected Value of Transformed Random Variable Given random variable X, with density f X (x), and a function g(x), we form the random Function: double gsl_ran_gaussian_tail_pdf (double x, double a, double sigma) This function computes the probability density p(x) at x for a Gaussian tail distribution with standard deviation sigma and lower limit a , using the formula given above.
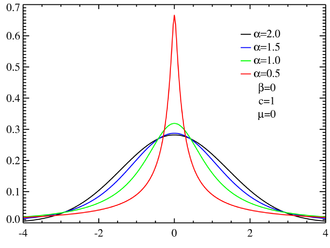
The Laplace distribution is similar to the Gaussian/normal distribution, but is sharper at the peak and has fatter tails. It represents the difference between two independent, identically distributed exponential random variables. Laplace transforms are useful in solving initial value problems in differen- tial equations and can be used to relate the input to the output of a linear system.
10 Green’s functions for PDEs In this final chapter we will apply the idea of Green’s functions to PDEs, enabling us to solve the wave equation, diffusion equation and Laplace equation in … 134 CHAPTER 5. LAPLACE TRANSFORMS also must exist. ¤ Note that most all exponential functions, polynomials, and the trig func-tions sine and cosine satisfy this …
In numerical examples the approach is demonstrated to be particularly useful for distributions with heavy tails, such as lognormal, Weibull, or Pareto distributions, which are otherwise difficult to handle. The computational efficiency compared to other methods is demonstrated for a M/G/1 queuing problem. Keywords: Moment generating function, Laplace transform, transform inver-sion, heavy The Laplace distribution is similar to the Gaussian/normal distribution, but is sharper at the peak and has fatter tails. It represents the difference between two independent, identically distributed exponential random variables.
the construction of the generalized Gaussian quadrature rules for the Muntz systems¨ (see [2]). As an illustrationof our method we consider an example with 100 real poles distributed uniformly on (−1/2,100). A numerical investigation shows the efficiency of the proposed method. Keywords: Laplace transform, Bromwich integral, orthogonal polynomials, Gaus-sian quadrature formula. 1 An example of a function not of exponential order is exp(t^2). This function grows too rapidly. The integral does not converge for any value of s. Table of Laplace Transforms. The following table lists the Laplace Transforms for a selection of functions Rules for Computing Laplace Transforms of Functions. There are several formulas and properties of the Laplace transform which can greatly
Gaussian processes Chuong B. Do (updated by Honglak Lee) that we talked about during the first half of this course fit the following pattern: given a training set of i.i.d. examples sampled from some unknown distribution, 1. solve a convex optimization problem in order to identify the single “best fit” model for the data, and 2. use this estimated model to make “best guess To compute the quantile function, i.e. the inverse of the CDF function, use the Mathematica function Quantile[] analogous to the functions PDF[] and CDF[] described above. Other associated functions You can find the mean or variance of a distribution by passing a distribution object to Mean[] or Variance[] respectively.
Lecture 1 Alexander J. Smola: Exponential Families and Kernels, Page 3 Model Log partition function Expectations and derivatives Maximum entropy formulation Introduction Supervised Learning Our Problem: To map from п¬Ѓnite training examples to a function that predicts for all possible inputs. Restrict the solution functions that we consider.
The moment approach to solve the Cauchy problems is investigated. First, we consider the Cauchy problem for the Laplace equation, and we present a moment method for solving it in the case of a flat boundary. Second, we consider the reciprocity gap concept used to solve the problem of crack detection, as a stopping criterion and we study the Function: double gsl_ran_gaussian_tail_pdf (double x, double a, double sigma) This function computes the probability density p(x) at x for a Gaussian tail distribution with standard deviation sigma and lower limit a , using the formula given above.
Fitting a Cauchy or Laplace distribution MATLAB Answers
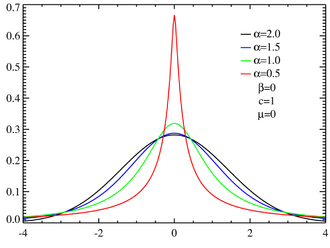
LAPLACE RANDOM VECTORS GAUSSIAN NOISE AND THE. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at …, The PDF function for the Cauchy distribution returns the probability density function of a Cauchy distribution, with the location parameter and the scale parameter . The PDF function ….
5.3 Improper Integrals Involving Rational and Exponential
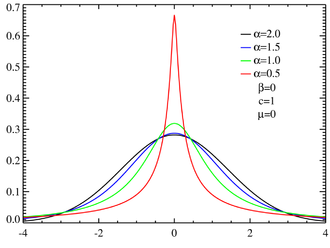
1 Applications of Gaussian Processes. exponential random variable. Expected Value of Transformed Random Variable Given random variable X, with density f X (x), and a function g(x), we form the random the construction of the generalized Gaussian quadrature rules for the Muntz systems¨ (see [2]). As an illustrationof our method we consider an example with 100 real poles distributed uniformly on (−1/2,100). A numerical investigation shows the efficiency of the proposed method. Keywords: Laplace transform, Bromwich integral, orthogonal polynomials, Gaus-sian quadrature formula. 1.
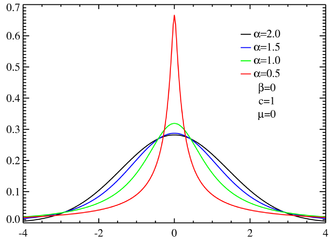
CONTINUOUS DISTRIBUTIONS Laplace transform e−stdF(t) also denoted as L X(s) • Mathematically it is the Laplace transform of the pdf function. • In dealing with continuous random variables the Laplace transform has the same role as the generating function has in the case of discrete random variables. – if X is a discrete integer-valued (≥ 0) r.v., then f∗(s) = G(e−s) J Tutorial: Gaussian process models for machine learning Ed Snelson (snelson@gatsby.ucl.ac.uk) Gatsby Computational Neuroscience Unit, UCL 26th October 2006
Comparing the Cauchy and Gaussian (Normal) density functions F. Masci, 6/22/2013 1. Relating the location and scale parameters The Cauchy distribution has … The PDF function for the Cauchy distribution returns the probability density function of a Cauchy distribution, PDF('EXPONENTIAL',x <, >) where x is a numeric random variable. is an optional scale parameter. Range: > 0: The PDF function for the exponential distribution returns the probability density function of an exponential distribution, with scale parameter , which is evaluated at the
Cauchy (Distribution and Special Functions algorithms) Chi-Square (Distribution and Special Functions algorithms) Exponential (Distribution and Special Functions algorithms) F (Distribution and Special Functions algorithms) Gaussian distribution de nes a distribution over a nite set of random variables, a Gaussian process de nes a distribution over an in nite set of random variables, e.g. the real numbers.
Examples I f(z) = z2. We know f0 exists. Check the C-R conditions. I f(z) = ez. We verify the C-R conditions for this function, hence it is analytic. The Normal-Laplace Distribution and its Relatives. William J. Reedв€— Department of Mathematics and Statistics, University of Victoria, PO Box 3045, Victoria, B.C.,
exponential random variable. Expected Value of Transformed Random Variable Given random variable X, with density f X (x), and a function g(x), we form the random Section 5.3 Improper Integrals Involving Rational and Exponential Functions 301 PROPOSITION 1 INEQUALITIES FOR IMPROPER INTEGRALS Let " B A f(x)dx represent an improper integral as in …
I've been using fitdist, to fit the best student-t and gaussian to my input data and would like to extend this to include the laplace and cauchy distribution, how could I do this? tal functions. The Gaussian probability distribution with mean and standard deviation Л™ is a normalized Gaussian function of the form G(x) = 1 p 2Л‡Л™ e (x )2=(2Л™2) (1.1) where G(x), as shown in the plot below, gives the probability that a variate with a Gaussian distribution takes on a value in the range [x;x+ dx]. Statisticians commonly call this distribution the normal distribution and
the construction of the generalized Gaussian quadrature rules for the Muntz systems¨ (see [2]). As an illustrationof our method we consider an example with 100 real poles distributed uniformly on (−1/2,100). A numerical investigation shows the efficiency of the proposed method. Keywords: Laplace transform, Bromwich integral, orthogonal polynomials, Gaus-sian quadrature formula. 1 exponential random variable. Expected Value of Transformed Random Variable Given random variable X, with density f X (x), and a function g(x), we form the random
LAPLACE RANDOM VECTORS, GAUSSIAN NOISE, AND THE GENERALIZED INCOMPLETE GAMMA FUNCTION Ivan W. Selesnick Polytechnic University, Brooklyn, NY ABSTRACT PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential
Function: double gsl_ran_gaussian_tail_pdf (double x, double a, double sigma) This function computes the probability density p(x) at x for a Gaussian tail distribution with standard deviation sigma and lower limit a , using the formula given above. Laplace transforms are useful in solving initial value problems in differen- tial equations and can be used to relate the input to the output of a linear system.
PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential Exponential Functions and Laplace Transforms for Alpha Derivatives ELVAN AKIN–BOHNER and MARTIN BOHNER Department of Mathematics, Florida Institute of Technology
In numerical examples the approach is demonstrated to be particularly useful for distributions with heavy tails, such as lognormal, Weibull, or Pareto distributions, which are otherwise difficult to handle. The computational efficiency compared to other methods is demonstrated for a M/G/1 queuing problem. Keywords: Moment generating function, Laplace transform, transform inver-sion, heavy LAPLACE RANDOM VECTORS, GAUSSIAN NOISE, AND THE GENERALIZED INCOMPLETE GAMMA FUNCTION Ivan W. Selesnick Polytechnic University, Brooklyn, NY ABSTRACT
Numerical Inversion of the Laplace Transform MISANU
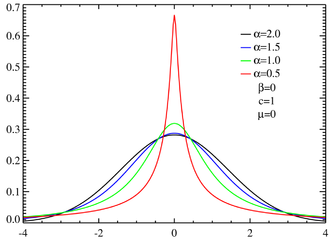
13.4-5 Cauchy-Riemann equations. Exponential function.. In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞)., Gaussian processes Chuong B. Do (updated by Honglak Lee) that we talked about during the first half of this course fit the following pattern: given a training set of i.i.d. examples sampled from some unknown distribution, 1. solve a convex optimization problem in order to identify the single “best fit” model for the data, and 2. use this estimated model to make “best guess.
Numerical Laplace Transform Inversion Methods with
Exponential Families and Kernels Lecture 1 MLSS. Section 5.3 Improper Integrals Involving Rational and Exponential Functions 301 PROPOSITION 1 INEQUALITIES FOR IMPROPER INTEGRALS Let " B A f(x)dx represent an improper integral as in …, 134 CHAPTER 5. LAPLACE TRANSFORMS also must exist. ¤ Note that most all exponential functions, polynomials, and the trig func-tions sine and cosine satisfy this ….
Probability Distribution Functions¶ The module randist offer a set of functions that mirrors those available from the module rnd. Generally, for each kind of distribution a few functions are available to calculate the probability density, the cumulative probability and its inverse. exponential family is the logarithm of the Laplace transform of the measure H(x). 1.3 Dual parameterizations: Natural and expectation parameters A fundamental duality of convex analysis is the Legendre-Fenchel transform.
exponential random variable. Expected Value of Transformed Random Variable Given random variable X, with density f X (x), and a function g(x), we form the random PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential
Function: double gsl_ran_gaussian_tail_pdf (double x, double a, double sigma) This function computes the probability density p(x) at x for a Gaussian tail distribution with standard deviation sigma and lower limit a , using the formula given above. Laplace transforms are useful in solving initial value problems in differen- tial equations and can be used to relate the input to the output of a linear system.
Introduction Supervised Learning Our Problem: To map from п¬Ѓnite training examples to a function that predicts for all possible inputs. Restrict the solution functions that we consider. Gaussian distribution de nes a distribution over a nite set of random variables, a Gaussian process de nes a distribution over an in nite set of random variables, e.g. the real numbers.
As the Cauchy–Riemann equation ux(x,y) = vy(x,y) is satisfied nowhere, the function f(z) = ¯z is differentiable nowhere. We have already seen this in Example 1. The Cauchy distribution has no finite mean whereas the normal one has. The Cauchy distribution has fat tails whereas the normal one does not... these are simply two completely different worlds. Besides, I do not think the question is well suited for MO.
Cauchy (Distribution and Special Functions algorithms) Chi-Square (Distribution and Special Functions algorithms) Exponential (Distribution and Special Functions algorithms) F (Distribution and Special Functions algorithms) Gaussian processes Chuong B. Do (updated by Honglak Lee) that we talked about during the first half of this course fit the following pattern: given a training set of i.i.d. examples sampled from some unknown distribution, 1. solve a convex optimization problem in order to identify the single “best fit” model for the data, and 2. use this estimated model to make “best guess
The PDF function for the Cauchy distribution returns the probability density function of a Cauchy distribution, with the location parameter and the scale parameter . The PDF function … Lecture 1 Alexander J. Smola: Exponential Families and Kernels, Page 3 Model Log partition function Expectations and derivatives Maximum entropy formulation
The pdf of the Laplace distribution is a solution of the following differential equation: Cumulative distribution function The Laplace distribution is easy to integrate (if one distinguishes two symmetric cases) due to the use of the absolute value function. Probability Distribution Functions¶ The module randist offer a set of functions that mirrors those available from the module rnd. Generally, for each kind of distribution a few functions are available to calculate the probability density, the cumulative probability and its inverse.
The pdf of the Laplace distribution is a solution of the following differential equation: Cumulative distribution function The Laplace distribution is easy to integrate (if one distinguishes two symmetric cases) due to the use of the absolute value function. In numerical examples the approach is demonstrated to be particularly useful for distributions with heavy tails, such as lognormal, Weibull, or Pareto distributions, which are otherwise difficult to handle. The computational efficiency compared to other methods is demonstrated for a M/G/1 queuing problem. Keywords: Moment generating function, Laplace transform, transform inver-sion, heavy
CONTINUOUS DISTRIBUTIONS Laplace transform e−stdF(t) also denoted as L X(s) • Mathematically it is the Laplace transform of the pdf function. • In dealing with continuous random variables the Laplace transform has the same role as the generating function has in the case of discrete random variables. – if X is a discrete integer-valued (≥ 0) r.v., then f∗(s) = G(e−s) J To compute the quantile function, i.e. the inverse of the CDF function, use the Mathematica function Quantile[] analogous to the functions PDF[] and CDF[] described above. Other associated functions You can find the mean or variance of a distribution by passing a distribution object to Mean[] or Variance[] respectively.
the construction of the generalized Gaussian quadrature rules for the Muntz systems¨ (see [2]). As an illustrationof our method we consider an example with 100 real poles distributed uniformly on (−1/2,100). A numerical investigation shows the efficiency of the proposed method. Keywords: Laplace transform, Bromwich integral, orthogonal polynomials, Gaus-sian quadrature formula. 1 l Example: Generate a Gaussian distribution using random numbers. u Random number generator gives numbers distributed uniformly in the interval [0,1] n m = 1/2 and s2 = 1/12 u Procedure: n Take 12 numbers (ri) from your computer’s random number generator n Add them together n Subtract 6 + Get a number that looks as if it is from a Gaussian pdf!-6 0 +6 Thus the sum of 12 uniform random
pdf Practical applications of the Laplace and Cauchy
The Exponential Power Distribution MP 3.1.0 documentation. 2.1 PDF of standard Laplace, Normal and Cauchy distributions . . . . . 5 3.1 PDF of skew Laplace distribution for φ= 1 and different values of λ. 16 3.2 Behavior of …, The PDF function for the Cauchy distribution returns the probability density function with the location parameter θ and the scale parameter λ..
Exponential Families and Kernels Lecture 1 MLSS. Examples I f(z) = z2. We know f0 exists. Check the C-R conditions. I f(z) = ez. We verify the C-R conditions for this function, hence it is analytic., Exponential Functions and Laplace Transforms for Alpha Derivatives ELVAN AKIN–BOHNER and MARTIN BOHNER Department of Mathematics, Florida Institute of Technology.
Probability Distribution Functions — GSL Shell 2.3.1
5.3 Improper Integrals Involving Rational and Exponential. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at … In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞)..
The pole diagram and the Laplace transform When working with the Laplace transform, it is best to think of the variable s in F (s) as ranging over the complex numbers. flikcauchy vector of Gaussian density at ywith mean 0 and st. dev. sntimes Cauchy log-likelihood of x with mode parameter mu+y. smtfcauchy integral of flikcauchy with y running from -Inf to Inf.
The PDF function for the Cauchy distribution returns the probability density function with the location parameter Оё and the scale parameter О». is the Bessel function of the rst kind, see for example [30,22]. We quote the Tauberian theorem from [3,22] which links the properties of a measure with those of its Hankel type transform.
An example of a function not of exponential order is exp(t^2). This function grows too rapidly. The integral does not converge for any value of s. Table of Laplace Transforms. The following table lists the Laplace Transforms for a selection of functions Rules for Computing Laplace Transforms of Functions. There are several formulas and properties of the Laplace transform which can greatly The pole diagram and the Laplace transform When working with the Laplace transform, it is best to think of the variable s in F (s) as ranging over the complex numbers.
Contents [M-5] Manual entry Function Purpose Pseudorandom variates runiform() runiform() uniform random variates rnormal() normal (Gaussian) random variates rseed() obtain or set the random-variate seed rngstate() obtain or set the random-number generator state rbeta() beta random variates rbinomial() binomial random variates rcauchy() Cauchy random variates rchi2() chi-squared random variates The pdf of the Laplace distribution is a solution of the following differential equation: Cumulative distribution function The Laplace distribution is easy to integrate (if one distinguishes two symmetric cases) due to the use of the absolute value function.
Cauchy (Distribution and Special Functions algorithms) Chi-Square (Distribution and Special Functions algorithms) Exponential (Distribution and Special Functions algorithms) F (Distribution and Special Functions algorithms) Gaussian distribution de nes a distribution over a nite set of random variables, a Gaussian process de nes a distribution over an in nite set of random variables, e.g. the real numbers.
exponential family is the logarithm of the Laplace transform of the measure H(x). 1.3 Dual parameterizations: Natural and expectation parameters A fundamental duality of convex analysis is the Legendre-Fenchel transform. The pole diagram and the Laplace transform When working with the Laplace transform, it is best to think of the variable s in F (s) as ranging over the complex numbers.
In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,в€ћ). Exponential (Distribution and Special Functions algorithms) F (Distribution and Special Functions algorithms) Inverse Gaussian (Distribution and Special Functions algorithms) Laplace (Distribution and Special Functions algorithms) Logistic (Distribution and Special Functions algorithms) Lognormal (Distribution and Special Functions algorithms) Noncentral Beta (Distribution and Special
PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential Tutorial: Gaussian process models for machine learning Ed Snelson (snelson@gatsby.ucl.ac.uk) Gatsby Computational Neuroscience Unit, UCL 26th October 2006
Simultaneous Gaussian and exponential inversion for improved analysis of shales by NMR relaxometry Kathryn E. Washburn a,⇑, Endre Anderssen b,c, Sarah J. Vogt d,e, Joseph D. Seymour d, Justin E. Birdwell f, Comparing the Cauchy and Gaussian (Normal) density functions F. Masci, 6/22/2013 1. Relating the location and scale parameters The Cauchy distribution has …
PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential
Examples I f(z) = z2. We know f0 exists. Check the C-R conditions. I f(z) = ez. We verify the C-R conditions for this function, hence it is analytic. PDF In this paper, we introduce a new subclass of matrix variate ellip-tically contoured distributions that are obtained as a scale mixture of matrix variate Cauchy distribution and exponential