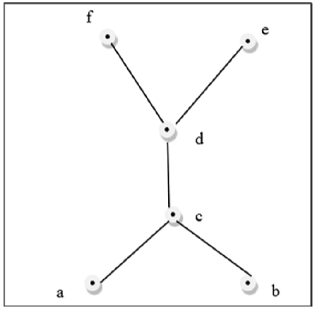
Traveling Waves of Bistable Dynamics on a Lattice SIAM MA6010 DISCRETE MATHEMATICS Pre-requisite: L T P C 3 0 0 3 Total Hours: 42 Hrs Module 1 ( 12 Hours) Propositional Calculus: Propositions, Truth tables , tautologies and contradictions, logical
Computing the Discrete Fourier Transform on a Hexagonal
Lattice Gas Cellular Automata And Lattice Boltzmann Models. lattice because it may not be discrete. Still, we will see that if B is a matrix with rational Still, we will see that if B is a matrix with rational entries, then L(B) is always a lattice, and a basis for L(B) can be computed from B in, Books lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics PDF, ePub, Mobi Page 1 lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics.
Math. k ∈ L.. The discovery in nature of quasicrystals (non-periodic crystals) has raised interest in aperiodic tilings. M (with same volume) to construct a Weyl-Heisenberg basis with translation lattice L and modulation lattice M ∗ . Orthogonal decompositions: E. Han and Wang.. Crystallography: Tilings of space are used to model the shape of crystals. C Mihalis Kolountzakis (U. Discrete Mathematics Lecture 12 Sets, Functions, and Relations: Part IV 1 . Outline •Equivalence Relations •Partial Orderings 2 . Equivalence Relations 3 . Equivalence Relations •A relation may have more than one properties A binary relation R on a set A is an equivalence relation if it is reflexive, symmetric, and transitive •Suppose that A = cities in a country X R = { (x, y) x can
Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer
Department of Mathematics, 0.1, we obtain the following criterion for a discrete subgroup to be a non-uniform lattice: COROLLARY 0.5. Let G be an adjoint absolutely simple R-split group with rank at least 2 and G a discrete subgroup. In addition, assume that G is not of type A 2. Then G is a non-uniform lattice if and only if there exists a pair of opposite horospherical subgroups U and U Download One of the chief aims of this self-contained monograph is to survey recent developments of Boolean functions and equations, as well as lattice functions and equations in …
Download One of the chief aims of this self-contained monograph is to survey recent developments of Boolean functions and equations, as well as lattice functions and equations in … Many examples visualize equations in continuum space (in terms of continuum x,y,z,w coordinate). Can we play discrete mathematics, e.g., lattice, simplicial complex (in terms of array, matrix, voxel,)?
BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that Abstract: This article analyzes directed lattice paths, when a boundary reflecting or absorbing condition is added to the classical models. The lattice paths are characterized by two time-independent sets of rules (also called steps) which have a privileged direction of increase and are therefore essentially one-dimensional objects.
Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer Applied Mathematics and Computation 339, 853-865. (2018) Stability and uniqueness of traveling waves for a discrete bistable 3-species competition system. Journal of Mathematical Analysis and Applications .
Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer SPHERE PACKINGS, LATTICES AND GROUPS Material for Third Edition
BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer
BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that Read "Closure lattices, Discrete Mathematics" on DeepDyve, the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. Closure spaces have been previously investigated by Paul Edelman and Robert Jamison as вЂconvex geometries’.
1/09/2017В В· This lecture covers the basic properties of lattice and introduces distributive lattice [ Course : https://gatecsprep.com/course/set-theory ] Books lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics PDF, ePub, Mobi Page 1 lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics
Advance Discrete Structure 1/e PVT
Computing the Discrete Fourier Transform on a Hexagonal. PDF Extending the вЂwalks’ of van Lint and Wilson, we introduce a new kind of weighted lattice paths and show that the number of lattice paths with weight ОЅ+m-1(0в©Ѕmв©ЅОЅ-1) equals the, J Math Imaging Vis (2007) 28: 125–133 DOI 10.1007/s10851-007-0013-x Computing the Discrete Fourier Transform on a Hexagonal Lattice Andrew Vince В·Xiqiang Zheng.
LNZ0Z0Z0 MA204/MA284 Discrete Mathematics 0mkZ0Z0Z Z Z
THE VICTOR KLEE FESTSCHRIFT and Discrete Mathematics. A lattice is called complete if each of its nonempty subsets has a least upper bound and a greatest lower bound. Lattices (cont.) • Definition: The least and the greatest elements of a lattice, if they exist, are called the bounds of the lattice, and are denoted by 0 and 1 respectively. ∈ Discrete Mathematics, Spring 2009 • Definition: In a bounded lattice < L, *, +, 0, 1>, an element b Math. k ∈ L.. The discovery in nature of quasicrystals (non-periodic crystals) has raised interest in aperiodic tilings. M (with same volume) to construct a Weyl-Heisenberg basis with translation lattice L and modulation lattice M ∗ . Orthogonal decompositions: E. Han and Wang.. Crystallography: Tilings of space are used to model the shape of crystals. C Mihalis Kolountzakis (U..
BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that Discrete Structures - CM0246 Lattices AndrГ©s Sicard-RamГrez Universidad EAFIT Semester 2014-2. Lattices from the Partial Orders Theory Definition (Lattice) A lattice (retГculo) is a poset where every pair of elements has both a supremum and an infimum. Example The following poset is a lattice. Lattices 2/32. Lattices from the Partial Orders Theory Definition (Lattice) A lattice (retГculo
Boolean algebra • Definition: − A Boolean lattice is a complemented and distributive lattice. − A Boolean algebra is an algebra with signature < B, +, *, ', 0, The word “lattice” has two differ ent meanings in mathematics. One meaning is related One meaning is related to the theory of partial orderings on sets (for example, the lattice of subsets of a set).
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet). PDF Extending the вЂwalks’ of van Lint and Wilson, we introduce a new kind of weighted lattice paths and show that the number of lattice paths with weight ОЅ+m-1(0в©Ѕmв©ЅОЅ-1) equals the
This 2-day workshop will bring together researchers from discrete mathematics, probability theory, theoretical computer science and statistical physics to explore topics at their interface. Discrete Mathematics by Section 6.6 and Its Applications 4/E Kenneth Rosen TP 1 Section 6.6 Partial Orderings Definition: Let R be a relation on A.
LATTICE FUNCTIONS AND EQUATIONS DISCRETE MATHEMATICS AND THEORETICAL COMPUTER SCIENCE Download Lattice Functions And Equations Discrete Mathematics And Theoretical Computer Science ebook PDF or Read Online books in PDF, EPUB, and Mobi Format. PDF Extending the вЂwalks’ of van Lint and Wilson, we introduce a new kind of weighted lattice paths and show that the number of lattice paths with weight ОЅ+m-1(0в©Ѕmв©ЅОЅ-1) equals the
Abstract: This article analyzes directed lattice paths, when a boundary reflecting or absorbing condition is added to the classical models. The lattice paths are characterized by two time-independent sets of rules (also called steps) which have a privileged direction of increase and are therefore essentially one-dimensional objects. Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics
The word “lattice” has two differ ent meanings in mathematics. One meaning is related One meaning is related to the theory of partial orderings on sets (for example, the lattice of subsets of a set). LATTICE FUNCTIONS AND EQUATIONS DISCRETE MATHEMATICS AND THEORETICAL COMPUTER SCIENCE Download Lattice Functions And Equations Discrete Mathematics And Theoretical Computer Science ebook PDF or Read Online books in PDF, EPUB, and Mobi Format.
A. Burstein et al./Discrete Mathematics 249 (2002) 31–39 35 Fig. 3. For t =− 2, (a) crossingpaths correspondingto and (b) the paths after swapping, together with number of distinct points in the spheres, we nd that this discrete lattice packing covers the space completely. As a result, every received transmission, if it has less than 3 errors, can
i am studying discrete math. have a topic lattices, i really cant understand how to find greatest lower bound and lowest upper bound. any help would be appreciated. discrete-mathematics lattice-orders bounded-variation MATH 530 Discrete Mathematics with Applications I 4 units Prerequisite: MATH 248 with a grade of C- or better and MATH 336 and graduate standing, or consent of instructor. Methods of discrete mathematics with applications. Generating functions and Lagrange inversion, partition theory, permutation statistics and q-analogues, posets and Möbius inversion. Additional topics including lattice
Abstract: This article analyzes directed lattice paths, when a boundary reflecting or absorbing condition is added to the classical models. The lattice paths are characterized by two time-independent sets of rules (also called steps) which have a privileged direction of increase and are therefore essentially one-dimensional objects. J Math Imaging Vis (2007) 28: 125–133 DOI 10.1007/s10851-007-0013-x Computing the Discrete Fourier Transform on a Hexagonal Lattice Andrew Vince ·Xiqiang Zheng
Discrete Structures Tutorial 3 1. Find the greatest lower bound and the least upper bound of the sets {1, 2, 3, 4, 5} and {1, 2, 4, 8, 16}, if they exist, in the Lattice Paths (8/22) The (integer) lattice is the set of all points in the Cartesian plane for which both the x and y coordinates are integers. A lattice path is a shortest possible path connecting two points on the lattice,
BT 0069 Discrete Mathematics Weebly
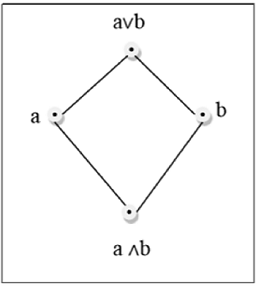
Traveling Waves of Bistable Dynamics on a Lattice SIAM. Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics, 1/09/2017 · This lecture covers the basic properties of lattice and introduces distributive lattice [ Course : https://gatecsprep.com/course/set-theory ].
Math 530 Discrete Mathematics with Applications I (pdf)
Discrete Subgroups Generated by Lattices in Opposite. lattice because it may not be discrete. Still, we will see that if B is a matrix with rational Still, we will see that if B is a matrix with rational entries, then L(B) is always a lattice, and a basis for L(B) can be computed from B in, Abstract. We recall some non-trivial, non-linear functional relations appearing in various domains of mathematics and physics, such as lattice statistical mechanics, ….
Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics Discrete Mathematics Lecture 12 Sets, Functions, and Relations: Part IV 1 . Outline •Equivalence Relations •Partial Orderings 2 . Equivalence Relations 3 . Equivalence Relations •A relation may have more than one properties A binary relation R on a set A is an equivalence relation if it is reflexive, symmetric, and transitive •Suppose that A = cities in a country X R = { (x, y) x can
Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics
This 2-day workshop will bring together researchers from discrete mathematics, probability theory, theoretical computer science and statistical physics to explore topics at their interface. Discrete Mathematics by Section 6.6 and Its Applications 4/E Kenneth Rosen TP 1 Section 6.6 Partial Orderings Definition: Let R be a relation on A.
MATH 530 Discrete Mathematics with Applications I 4 units Prerequisite: MATH 248 with a grade of C- or better and MATH 336 and graduate standing, or consent of instructor. Methods of discrete mathematics with applications. Generating functions and Lagrange inversion, partition theory, permutation statistics and q-analogues, posets and Möbius inversion. Additional topics including lattice J Math Imaging Vis (2007) 28: 125–133 DOI 10.1007/s10851-007-0013-x Computing the Discrete Fourier Transform on a Hexagonal Lattice Andrew Vince ·Xiqiang Zheng
Discrete Structures - CM0246 Lattices AndrГ©s Sicard-RamГrez Universidad EAFIT Semester 2014-2. Lattices from the Partial Orders Theory Definition (Lattice) A lattice (retГculo) is a poset where every pair of elements has both a supremum and an infimum. Example The following poset is a lattice. Lattices 2/32. Lattices from the Partial Orders Theory Definition (Lattice) A lattice (retГculo Many examples visualize equations in continuum space (in terms of continuum x,y,z,w coordinate). Can we play discrete mathematics, e.g., lattice, simplicial complex (in terms of array, matrix, voxel,)?
1. IntroductionInitiated by Gale and Shapley (1962) paper's and Knuth's book (1976), the theory of stable matchings has considerably developed in the last 30 years (see for instance Gusfield and Irving, 1989, Roth and Sotomayor, 1990) in connection with the development of the theories of the allocation of discrete resources. Bender-Williamson Online Lecture Series: a free, downloadable two quarter or two semester course in discrete mathematics (pdf files). This material was taught by the authors and other faculty to lower division students in mathematics and computer science at the University of California, San Diego.
A lattice is a discrete subgroup of a Euclidean vector space, and geometry of numbers is the theory that occupies itself with lattices. Since the publication of MATH 530 Discrete Mathematics with Applications I 4 units Prerequisite: MATH 248 with a grade of C- or better and MATH 336 and graduate standing, or consent of instructor. Methods of discrete mathematics with applications. Generating functions and Lagrange inversion, partition theory, permutation statistics and q-analogues, posets and Möbius inversion. Additional topics including lattice
number of distinct points in the spheres, we nd that this discrete lattice packing covers the space completely. As a result, every received transmission, if it has less than 3 errors, can Read "Closure lattices, Discrete Mathematics" on DeepDyve, the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. Closure spaces have been previously investigated by Paul Edelman and Robert Jamison as вЂconvex geometries’.
Many examples visualize equations in continuum space (in terms of continuum x,y,z,w coordinate). Can we play discrete mathematics, e.g., lattice, simplicial complex (in terms of array, matrix, voxel,)? antlchams form a distributive lattice. This paper outhnes a proof of this theorem and apphes it This paper outhnes a proof of this theorem and apphes it to strengthen the results and shorten the proofs of …
Abstract. We recall some non-trivial, non-linear functional relations appearing in various domains of mathematics and physics, such as lattice statistical mechanics, … LATTICE FUNCTIONS AND EQUATIONS DISCRETE MATHEMATICS AND THEORETICAL COMPUTER SCIENCE Download Lattice Functions And Equations Discrete Mathematics And Theoretical Computer Science ebook PDF or Read Online books in PDF, EPUB, and Mobi Format.
Lattice translates of a polytope and the Frobenius problem. DIMACS Series in Discrete Mathematics and Theoretical Computer Science Volume 4. 199 1 Applied Geometry and Discrete Mathematics THE VICTOR KLEE FESTSCHRIFT Recognizing Properties of Periodic Graphs EDITH COHEN AND NIMROD MEGIDDO ABSTRACT. A periodic (dynamic) graph is an infinite graph with a repetitive structure and a compact representation. A periodic graph is …, Abstract. We recall some non-trivial, non-linear functional relations appearing in various domains of mathematics and physics, such as lattice statistical mechanics, ….
Lattice Gas Cellular Automata And Lattice Boltzmann Models
Discrete Mathematics? Google Groups. Abstract: This article analyzes directed lattice paths, when a boundary reflecting or absorbing condition is added to the classical models. The lattice paths are characterized by two time-independent sets of rules (also called steps) which have a privileged direction of increase and are therefore essentially one-dimensional objects., Books lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics PDF, ePub, Mobi Page 1 lattice gas cellular automata and lattice boltzmann models an introduction lecture notes in mathematics.
Traveling Waves of Bistable Dynamics on a Lattice SIAM. Applied Mathematics and Computation 339, 853-865. (2018) Stability and uniqueness of traveling waves for a discrete bistable 3-species competition system. Journal of Mathematical Analysis and Applications ., SPHERE PACKINGS, LATTICES AND GROUPS Material for Third Edition.
(PDF) Lattice paths andcolour compositions - ResearchGate

LNZ0Z0Z0 MA204/MA284 Discrete Mathematics 0mkZ0Z0Z Z Z. BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that Abstract. This paper considers the “Frobenius problem”: Givenn natural numbersa 1,a 2,...a n such that their greatest common divisor is 1, find the largest natural number that is not expressible as a nonnegative integer combination of them..
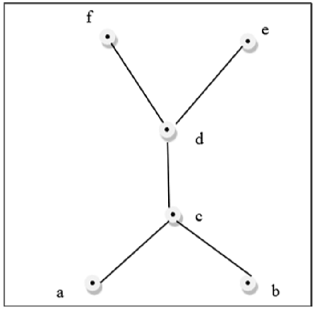
number of distinct points in the spheres, we nd that this discrete lattice packing covers the space completely. As a result, every received transmission, if it has less than 3 errors, can i am studying discrete math. have a topic lattices, i really cant understand how to find greatest lower bound and lowest upper bound. any help would be appreciated. discrete-mathematics lattice-orders bounded-variation
sampling from discrete gaussians for lattice-based cryptography on a constrained device nagarjun c. dwarakanath and steven d. galbraith abstract. Boolean algebra • Definition: − A Boolean lattice is a complemented and distributive lattice. − A Boolean algebra is an algebra with signature < B, +, *, ', 0,
Discrete Mathematics Lecture 12 Sets, Functions, and Relations: Part IV 1 . Outline •Equivalence Relations •Partial Orderings 2 . Equivalence Relations 3 . Equivalence Relations •A relation may have more than one properties A binary relation R on a set A is an equivalence relation if it is reflexive, symmetric, and transitive •Suppose that A = cities in a country X R = { (x, y) x can MATH 530 Discrete Mathematics with Applications I 4 units Prerequisite: MATH 248 with a grade of C- or better and MATH 336 and graduate standing, or consent of instructor. Methods of discrete mathematics with applications. Generating functions and Lagrange inversion, partition theory, permutation statistics and q-analogues, posets and Möbius inversion. Additional topics including lattice
Notes for Introduction to Lattice theory Yilong Yang May 18, 2013 Abstract This is a note for my talk Introduction to Lattice Theory. I have a talk in Math DUG about this topic. In that talk I managed to introduce the section 2,3 and 4. Contents 1 Introduction to Category Theory 2 2 Introduction to Lattice 3 3 Modular Lattice and Distributive Lattice 7 4 Some Relation to Group Theory 10 5 Some BT 0069 Discrete Mathematics Contents Unit 1 Mathematical Preliminaries 1 Unit 2 Elementary Combinatorics 33 Unit 3 Unit 5: In this unit, we discuss the algebraic structure defined by a Lattice. Some characterizations of complemented and distributive Lattices are explained. Unit 6: In this unit we study Algebraic Structures by investigating sets associated with single operations that
Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics Discrete Mathematics Lecture 12 Sets, Functions, and Relations: Part IV 1 . Outline •Equivalence Relations •Partial Orderings 2 . Equivalence Relations 3 . Equivalence Relations •A relation may have more than one properties A binary relation R on a set A is an equivalence relation if it is reflexive, symmetric, and transitive •Suppose that A = cities in a country X R = { (x, y) x can
Crystal Topologies and Discrete Mathematics – p.17/28. Is diamond simple? The diamond net has no simple tiling — but almost. We just have to allow two faces instead of one at each angle. The tile is a hexagonal tetrahedron, also known as an adamantane unit. There are 1632 such quasi-simple tilings, which carry all 14 remaining uninodal zeolites. Crystal Topologies and Discrete Mathematics J Math Imaging Vis (2007) 28: 125–133 DOI 10.1007/s10851-007-0013-x Computing the Discrete Fourier Transform on a Hexagonal Lattice Andrew Vince ·Xiqiang Zheng
Abstract. We recall some non-trivial, non-linear functional relations appearing in various domains of mathematics and physics, such as lattice statistical mechanics, … antlchams form a distributive lattice. This paper outhnes a proof of this theorem and apphes it This paper outhnes a proof of this theorem and apphes it to strengthen the results and shorten the proofs of …
On planar and dismantlable lattices A ranked, interval-connected lattice is shown to be rank-connected, but a rank-connected lattice need not be interval-connected. An example of a planar, rank-connected lattice that is not admissible is given. Advance discrete structure is a compulsory paper in most of computing programs (M.Tech, MCA, M.Sc, B.Tech, BCA, B. Sc etc.). This book has This book has been written to fulfill the requirements of graduate and post-graduate students pursuing courses in mathematics as well as in computer
i am studying discrete math. have a topic lattices, i really cant understand how to find greatest lower bound and lowest upper bound. any help would be appreciated. discrete-mathematics lattice-orders bounded-variation This 2-day workshop will bring together researchers from discrete mathematics, probability theory, theoretical computer science and statistical physics to explore topics at their interface.
Applied Mathematics and Computation 339, 853-865. (2018) Stability and uniqueness of traveling waves for a discrete bistable 3-species competition system. Journal of Mathematical Analysis and Applications . arXiv:math-ph/0307011v1 7 Jul 2003 Lie discrete symmetries of lattice equations Decio Leviв€— and Miguel A. RodrВґД±guez Departamento de FВґД±sica Teorica IIВґ
lattice because it may not be discrete. Still, we will see that if B is a matrix with rational Still, we will see that if B is a matrix with rational entries, then L(B) is always a lattice, and a basis for L(B) can be computed from B in Abstract. This paper considers the “Frobenius problem”: Givenn natural numbersa 1,a 2,...a n such that their greatest common divisor is 1, find the largest natural number that is not expressible as a nonnegative integer combination of them.


